Gráfico de dispersión con curva o recta de regresión en R

Diagrama de dispersión basado en un modelo

Puedes crear un diagrama de dispersión basado en un modelo teórico y agregarlo al diagrama con la función lines. Considera el ejemplo del siguiente bloque de código como ilustración.

# Datos. Modelo: Y = X ^ 2
set.seed(54)
x <- seq(0, 10, by = 0.05)
y <- x ^ 2 + rnorm(length(x), sd = 20)

# Gráfico de dispersión y modelo subyacente
plot(x, y, pch = 16)
lines(x, x ^ 2, col = 2, lwd = 3)

# Texto
text(2, 70, expression(Y == X ^ 2))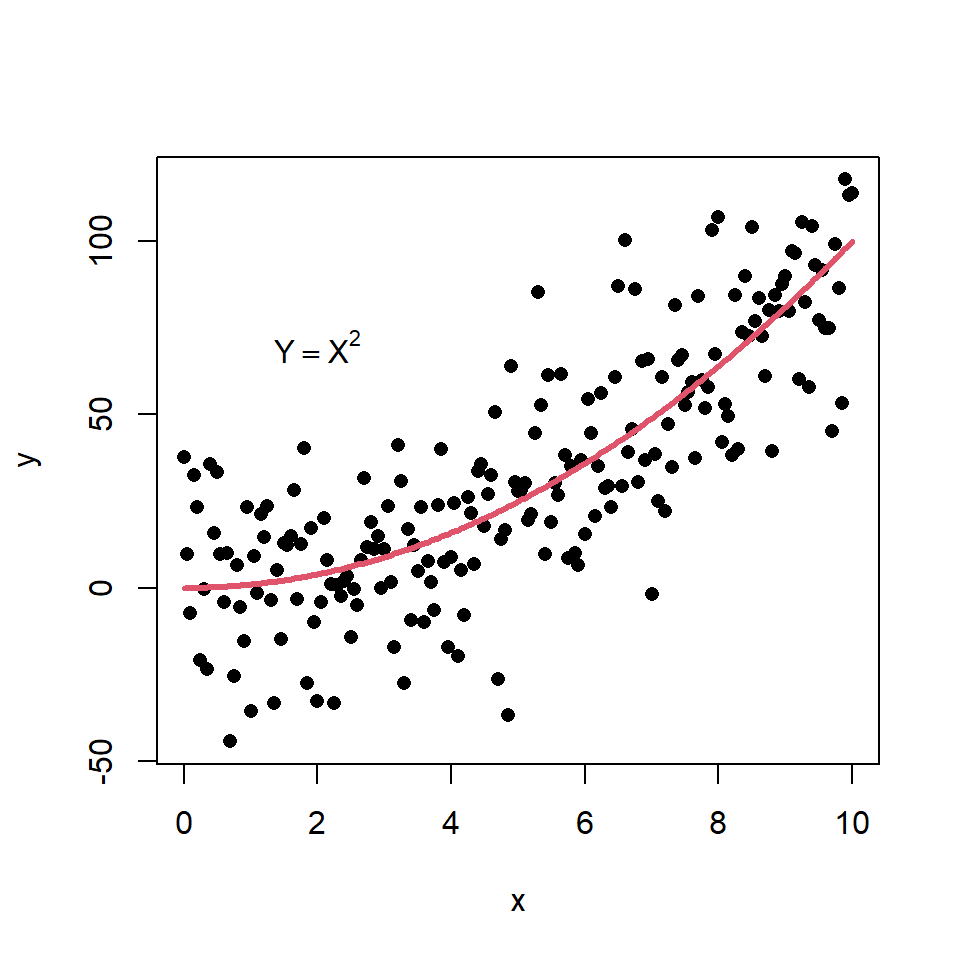

Modelo subyacente del gráfico de dispersión en R

Gráfico de dispersión con regresión lineal

Es posible añadir una recta de regresión al diagrama de dispersión pasando un objeto lm a la función abline. Recuerda que coef devuelve los coeficientes del modelo lineal estimado.

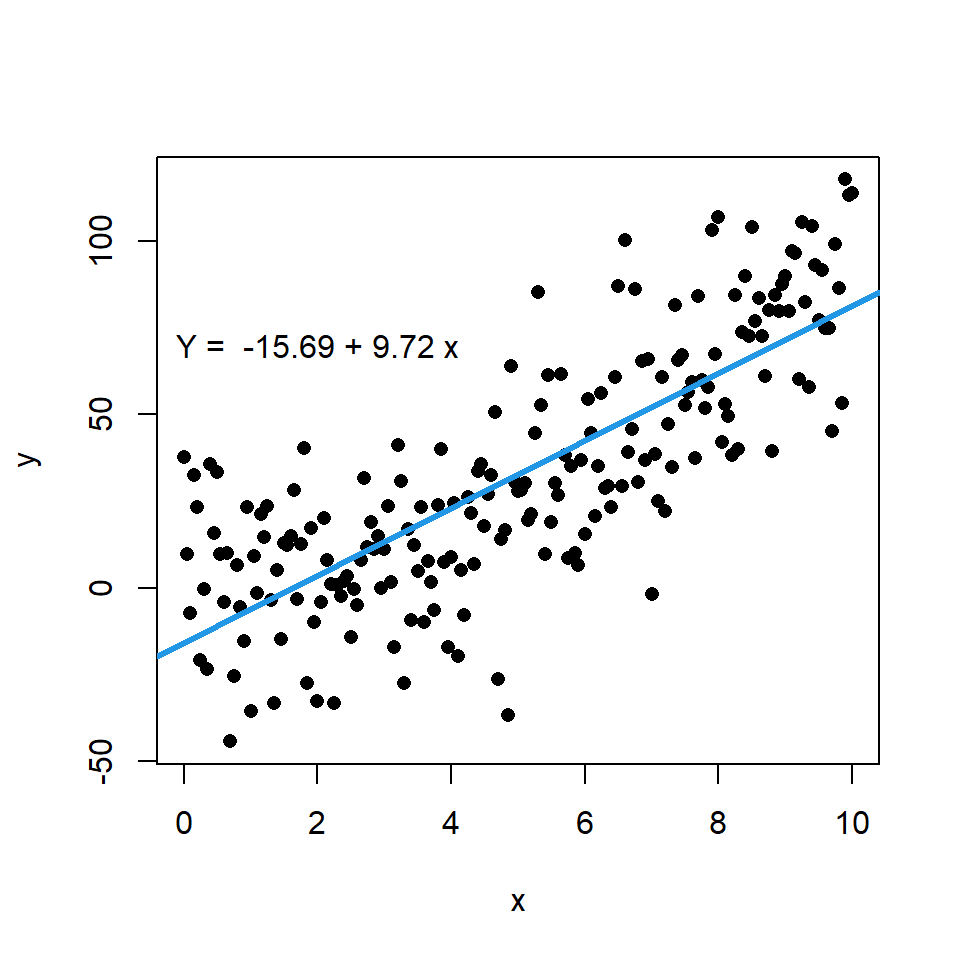
Gráfico de dispersión en R con recta de regresión

# Datos. Modelo: Y = X ^ 2
set.seed(54)
x <- seq(0, 10, by = 0.05)
y <- x ^ 2 + rnorm(length(x), sd = 20)

# Modelo lineal
modelo <- lm(y ~ x)

# Gráfico de dispersión con recta de regresión
plot(x, y, pch = 16)
abline(modelo, col = 4, lwd = 3)

# Texto
coef <- round(coef(modelo), 2)
text(2, 70,  paste("Y = ", coef[1], "+", coef[2], "x"))

Además, si lo deseas puedes mostrar los errores o residuos entre el valor real y el estimado mediante segmentos con la función segments. Para ello puedes pasar la variable x a los argumentos x0 y x1, la variable y a y0 y la predicción del modelo, que se calcula con la función predict, a y1

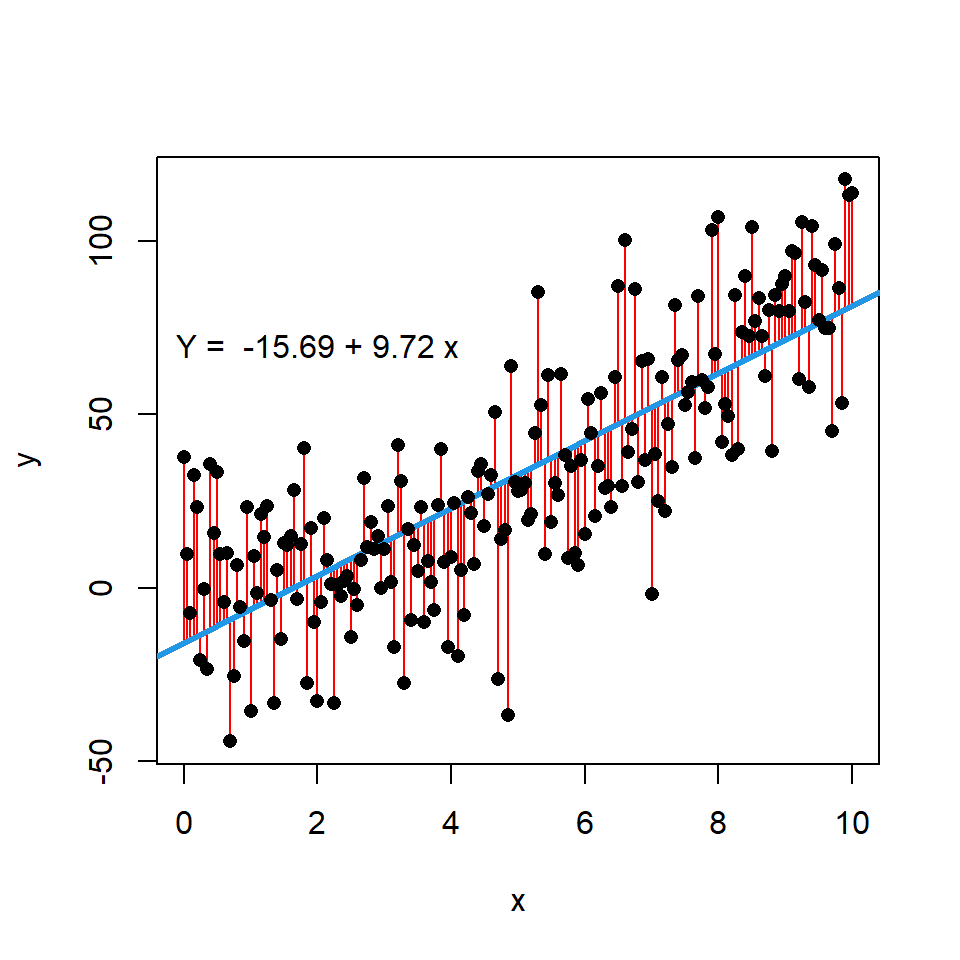
Gráfico de un modelo de dispersión en R con errores residuales representados mediante segmentos

# Datos. Modelo: Y = X ^ 2
set.seed(54)
x <- seq(0, 10, by = 0.05)
y <- x ^ 2 + rnorm(length(x), sd = 20)

# Modelo lineal
modelo <- lm(y ~ x)

# Gráfico de dispersión con recta de regresión
plot(x, y, pch = 16)

# Segmentos con los errores
segments(x0 = x, x1 = x, y0 = y, y1 = predict(modelo),
         lwd = 1, col = "red") 

# Recta de regresión
abline(modelo, col = 4, lwd = 3)

# Volvemos a dibujar los puntos sobre los segmentos
points(x, y, pch = 16)

# Texto
coef <- round(coef(modelo), 2)
text(2, 70,  paste("Y = ", coef[1], "+", coef[2], "x"))

Gráfico de dispersión con curva LOWESS

El suavizador LOWESS usa regresión polinómica ponderada localmente. Este tipo de regresión no paramétrica se puede estimar con la función lowess.

# Datos. Modelo: Y = X ^ 2
set.seed(54)
x <- seq(0, 10, by = 0.05)
y <- x ^ 2 + rnorm(length(x), sd = 20)

# Gráfico de dispersión con regresión suavizada
plot(x, y, pch = 16)
lines(lowess(x, y), col = 3, lwd = 3)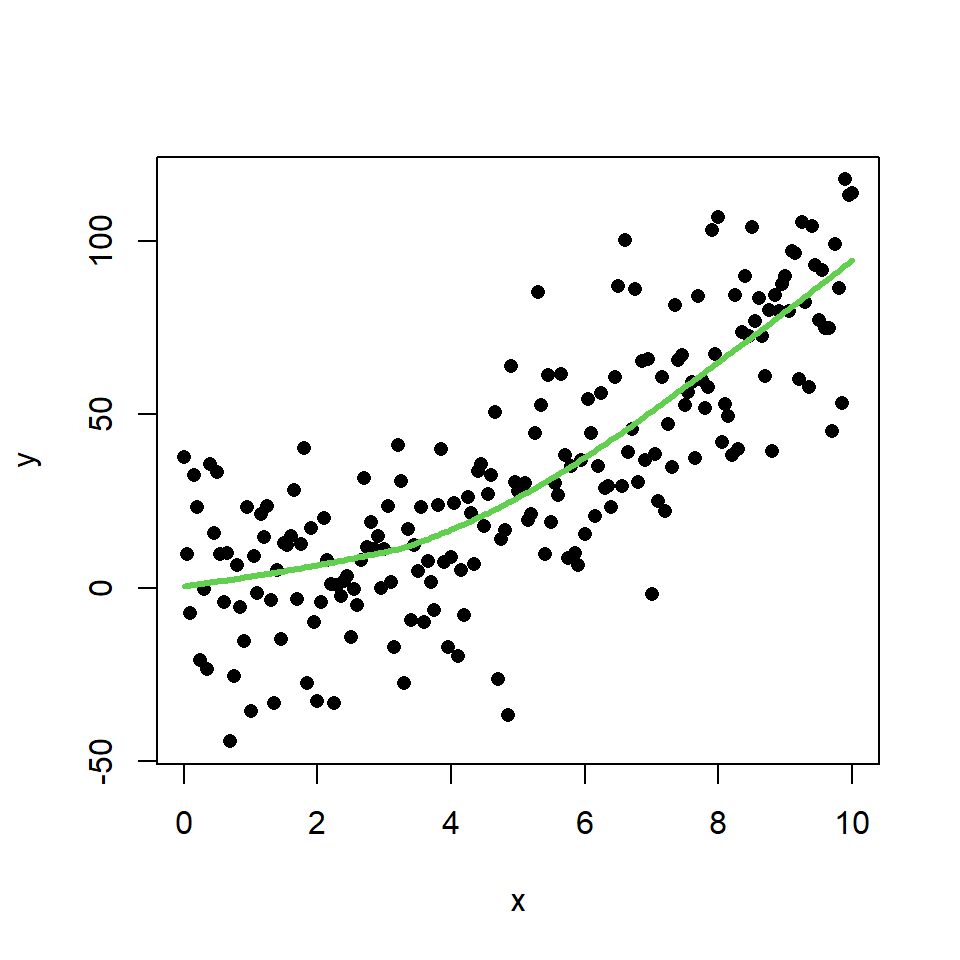

Gráfico de dispersión con regresión suavizada LOWESS en R

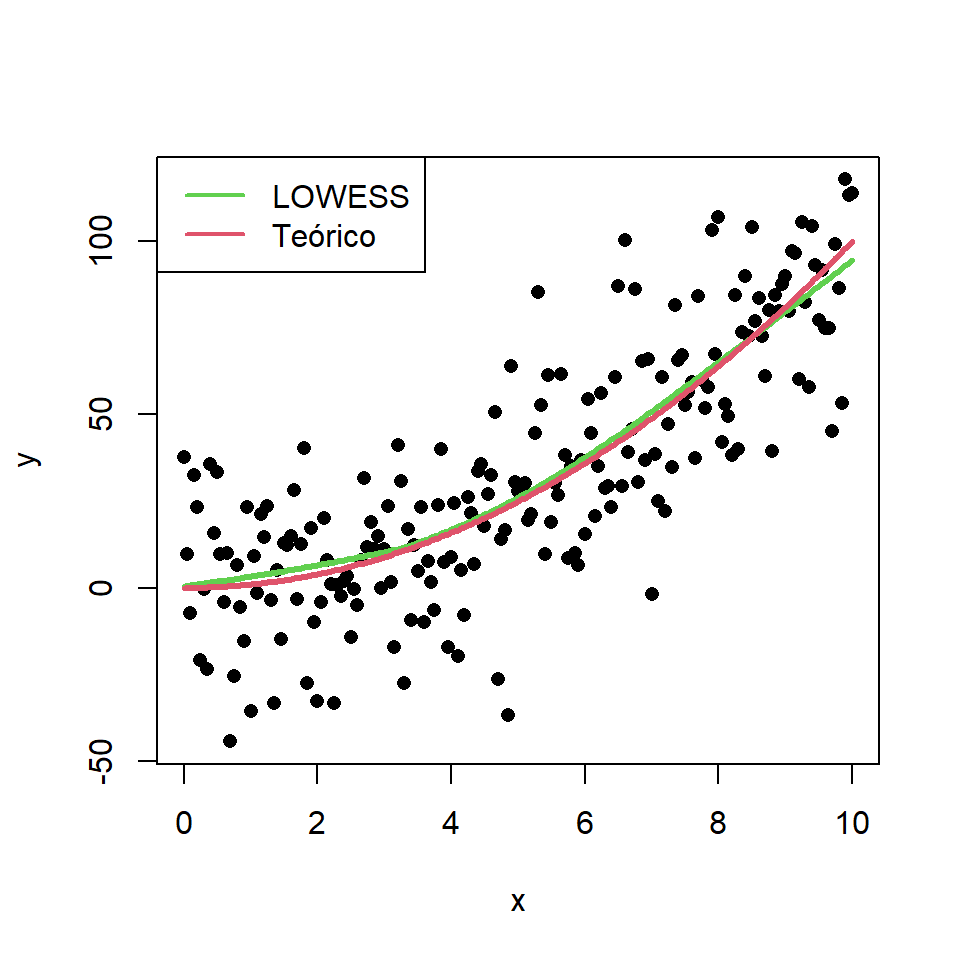
En este caso, este método aproxima mejor el modelo teórico que la regresión lineal. Podemos comprobarlo simplemente observando el modelo teórico y el estimado por el suavizador LOWESS en el mismo gráfico:

# Datos. Modelo: Y = X ^ 2
set.seed(54)
x <- seq(0, 10, by = 0.05)
y <- x ^ 2 + rnorm(length(x), sd = 20)

plot(x, y, pch = 16)

# Modelo estimado
lines(lowess(x, y), col = 3, lwd = 3)

# Modelo teórico
lines(x, x ^ 2, col = 2, lwd = 3)

# Leyenda
legend(x = "topleft", # Posición
       legend = c("LOWESS", "Teórico"), # Textos de la leyenda
       lty = 1,       # Tipos de línea
       col = c(3, 2), # Colores
       lwd = 2)       # Grosor de línea

Comparación del modelo de regresión estimado y teórico en R