Cleveland dot plot in R

Sample data

The following variables represent the quantity sold of a product every month of the year, the month and the quarter of the year for each month.

# Sample dataset
set.seed(1)
sold <- sample(400:450, 12)
month <- month.name
quarter <- c(rep(1, 3), rep(2, 3),
             rep(3, 3), rep(4, 3))

Basic dot plot with `dotchart` function

Basic dot chart

A dot plot can be created with the dotchart function from base R graphics. You can pass a vector of numeric values to the function to create the most basic chart.

dotchart(sold)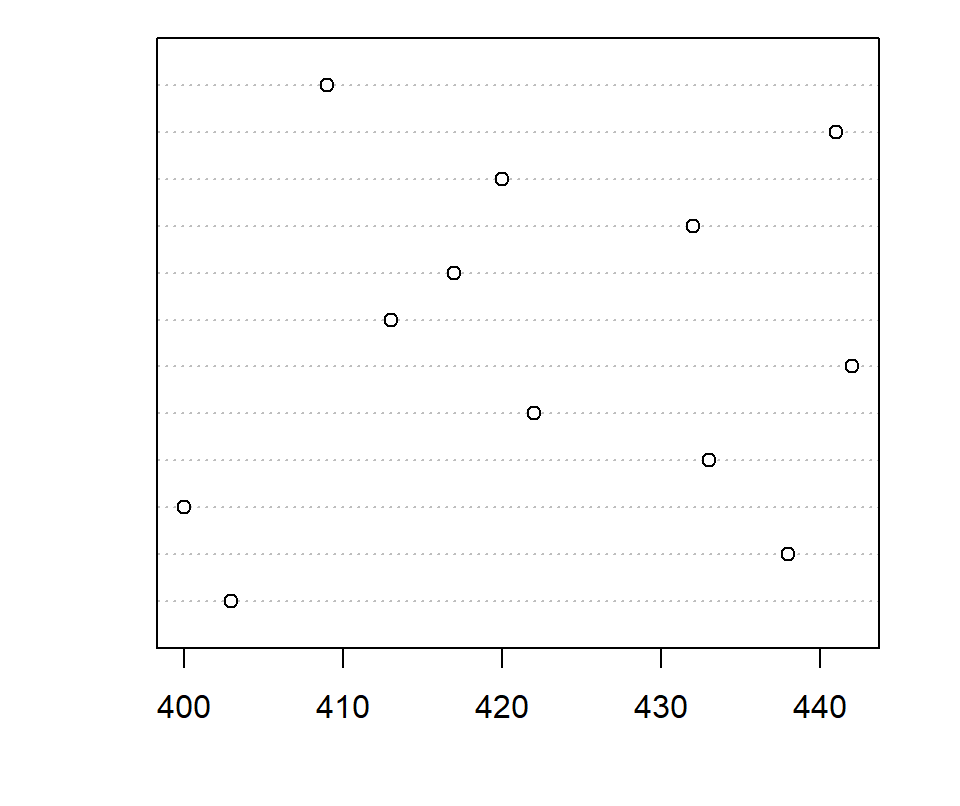

Basic dot chart in R

Customization

There are several arguments that can be customized, such as pch to change the plotting character symbol, col to change the color of the symbols, pt.cex for the size of the symbols and fram.plot, which is a logical determining whether to draw a box around the plot or not.

dotchart(sold,
         pch = 19,             # Symbol
         col = hcl.colors(12), # Colors
         pt.cex = 1.5,         # Symbol size
         frame.plot = TRUE)    # Plot frame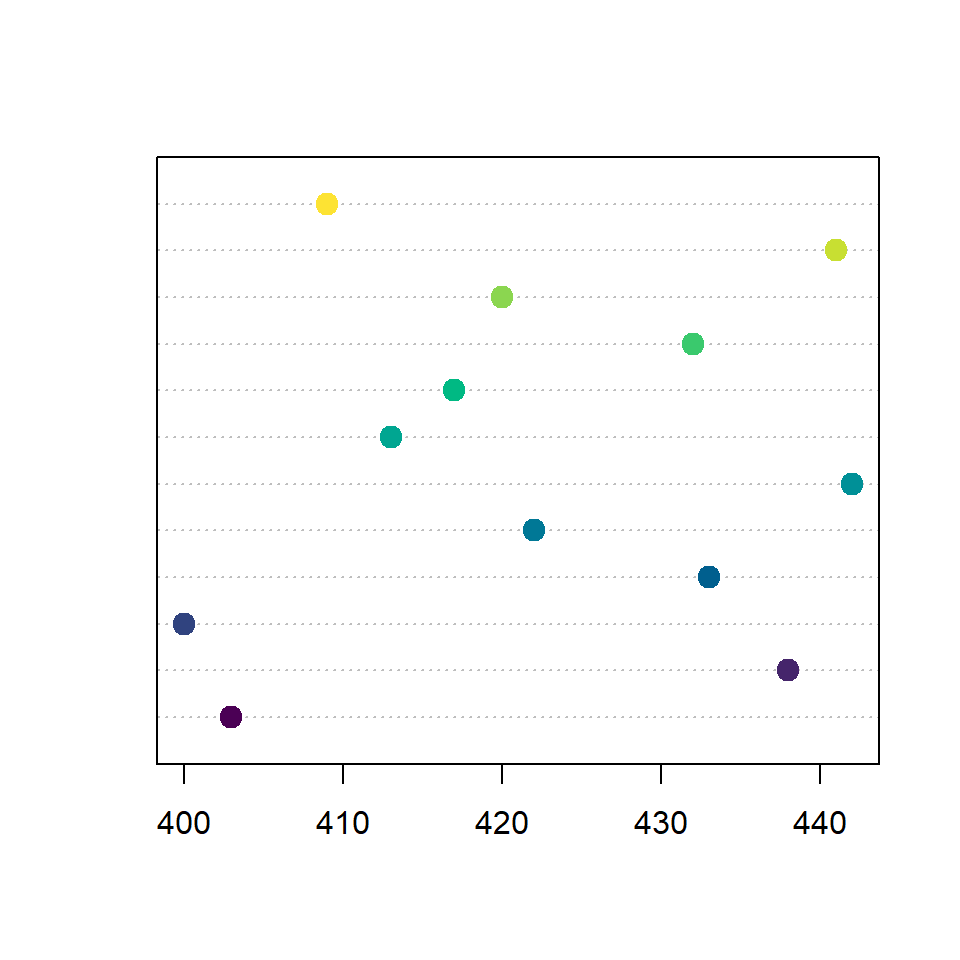

Dot plot in R

Labeling the observations

You can label each point with the labels argument. In this example we are passing the names of the months to represent each observation.

dotchart(sold,
         pch = 19,
         col = 4,
         pt.cex = 1.5,
         labels = month)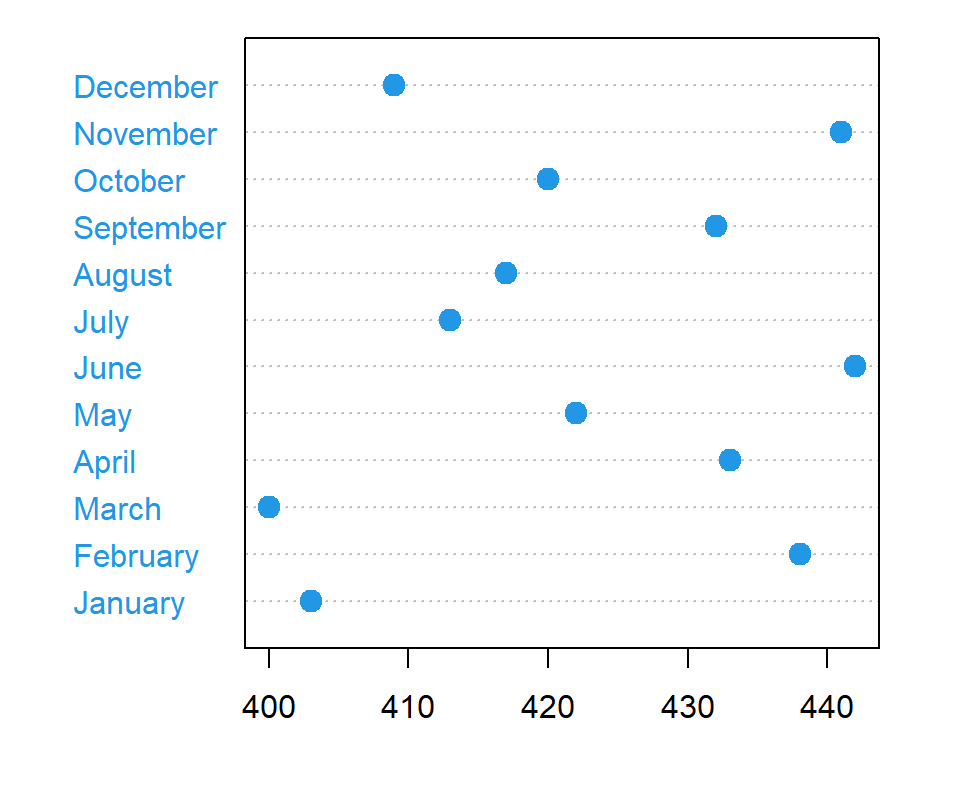

Cleveland dot plot in R with labels

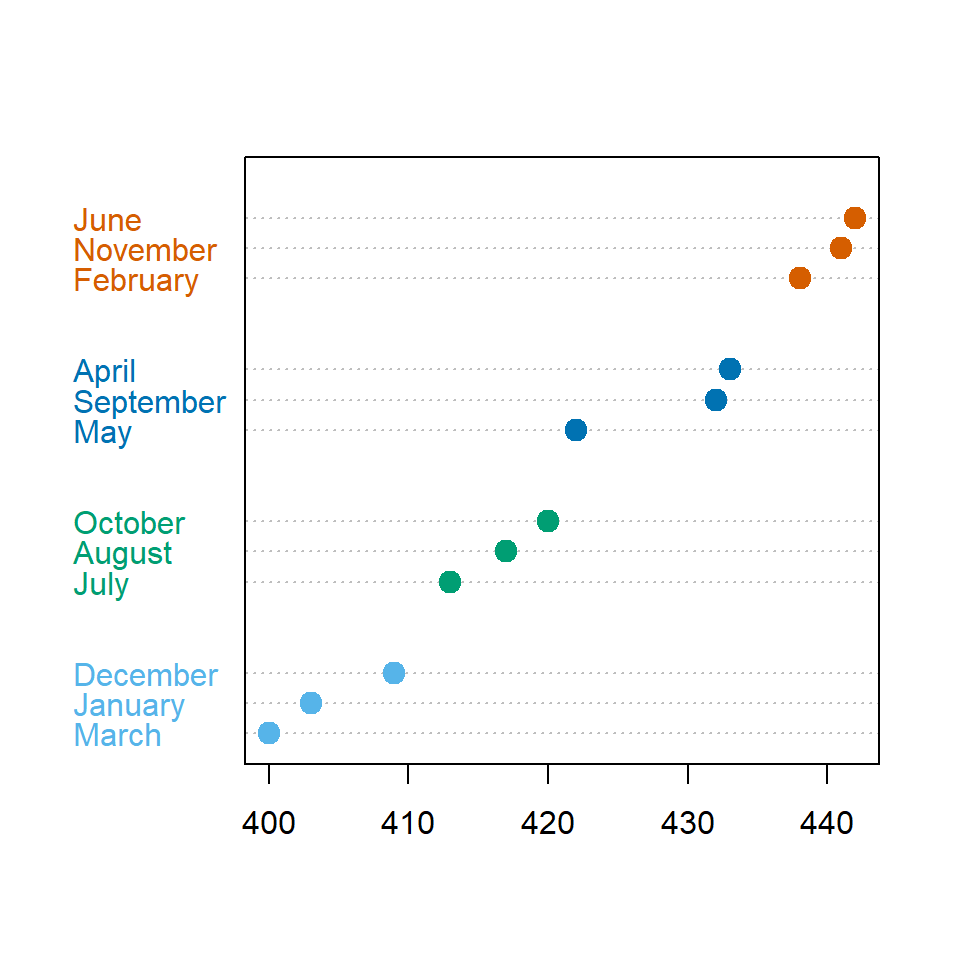
Dot chart by group

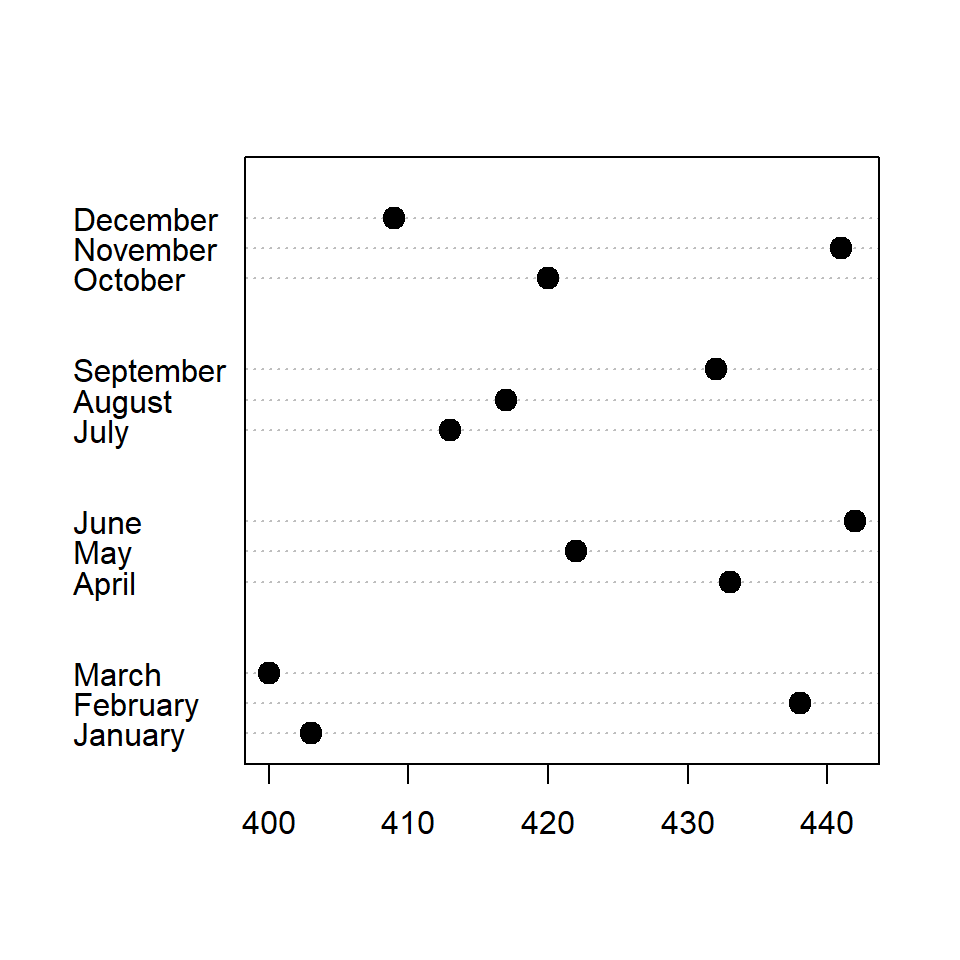
Cleveland dot plot by group in R

Specifying groups

Given a variable representing groups it is possible to group the elements. In the following example we are passing the quarter variable to the groups argument to group the months by quarter.

dotchart(sold,
         pch = 19, pt.cex = 1.5,
         labels = month,
         groups = rev(quarter))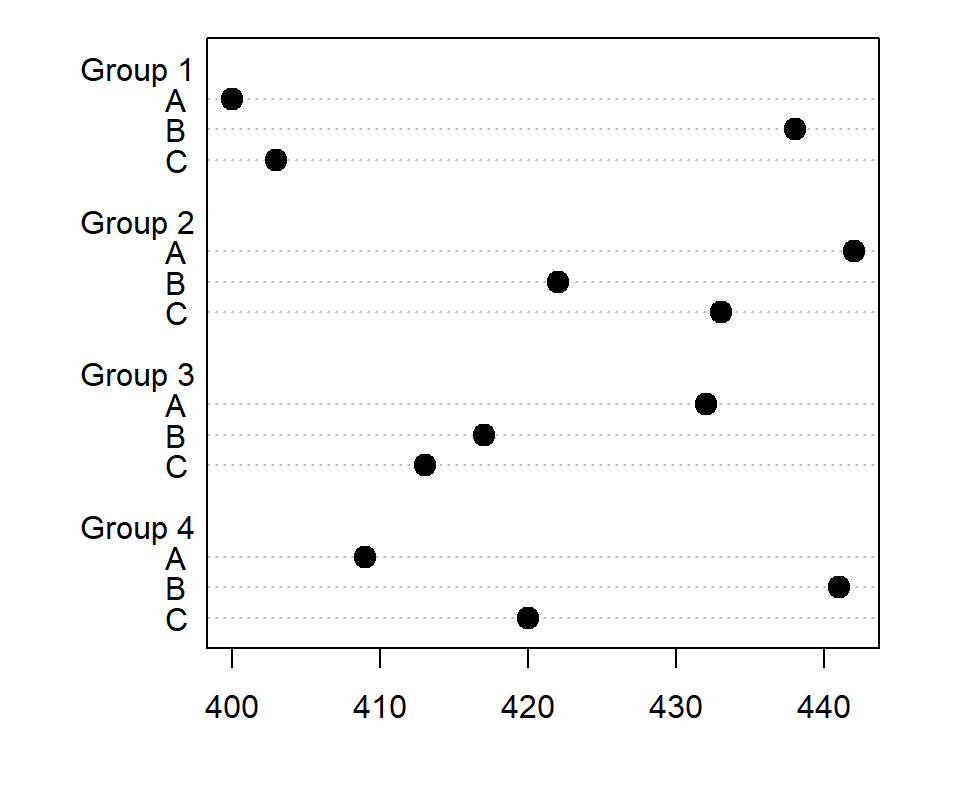

Dot plot in R based on a matrix

Matrix as input

Note that the dotchart function also allows passing a matrix. In this scenario the groups will be the columns of the matrix by default and the rows the observations for each group.

# Matrix from the data
m <- matrix(sold, ncol = 4)
colnames(m) <- c("G1", "G2", "G3", "G4")
rownames(m) <- LETTERS[3:1]

dotchart(m, pch = 19, pt.cex = 1.5)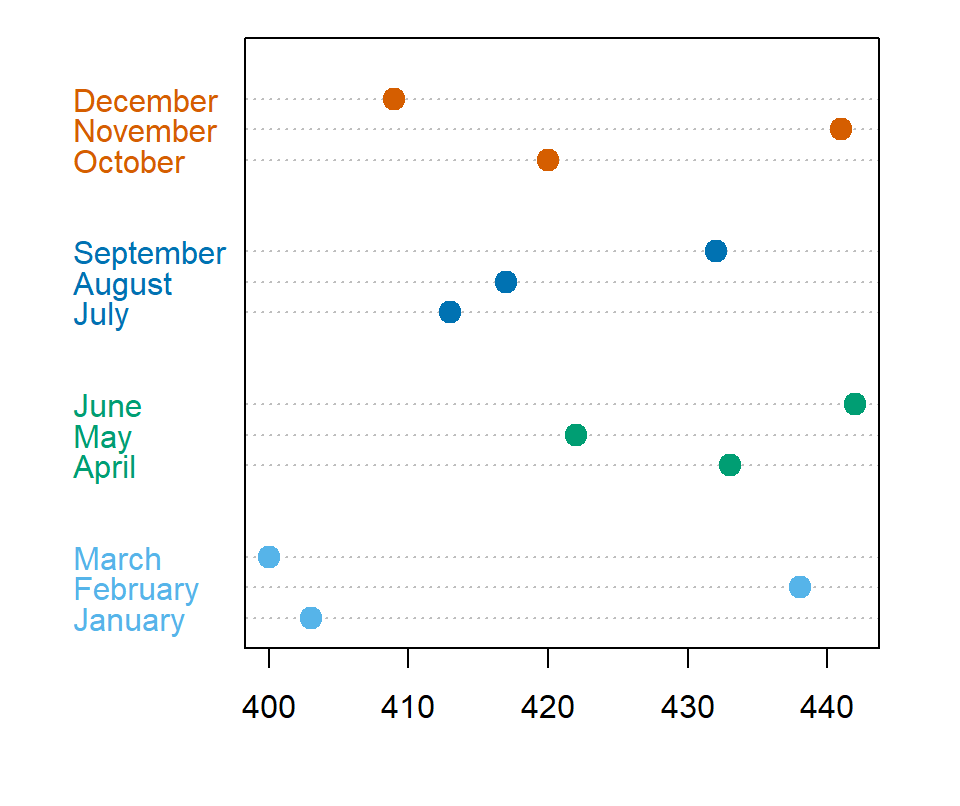

dotchart function with colors by group

Color by group

If you have passed a grouping variable to groups you can also customize the colors for each group, passing a vector of the same length of the input data to the color argument.

# Colors for each group
cols <- c(rep("#56B4E9", 3), rep("#009E73", 3),
          rep("#0072B2", 3), rep("#D55E00", 3))

dotchart(sold,
         pch = 19, pt.cex = 1.5,
         labels = month,
         groups = rev(quarter),
         color = cols)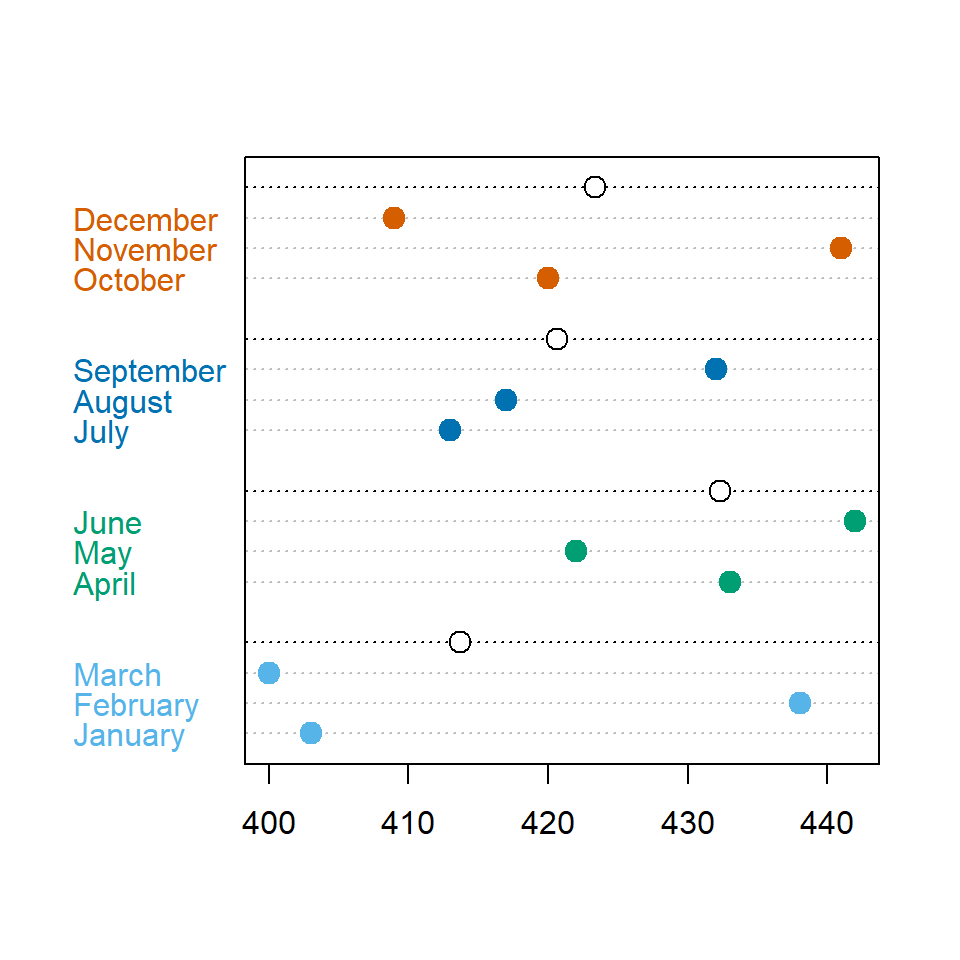

Adding a summary for each group with gdata argument

Summary for each group

The gdata argument allows passing some measure for the groups, such as a statistical summary. In the example below we are calculating the mean of sells by quarter.

# Colors for each group
cols <- c(rep("red", 3), rep("blue", 3),
          rep("green", 3), rep("orange", 3))

dotchart(sold,
         pch = 19, pt.cex = 1.5,
         labels = month,
         groups = rev(quarter),
         color = cols,
         gdata = rev(tapply(sold, quarter, mean)))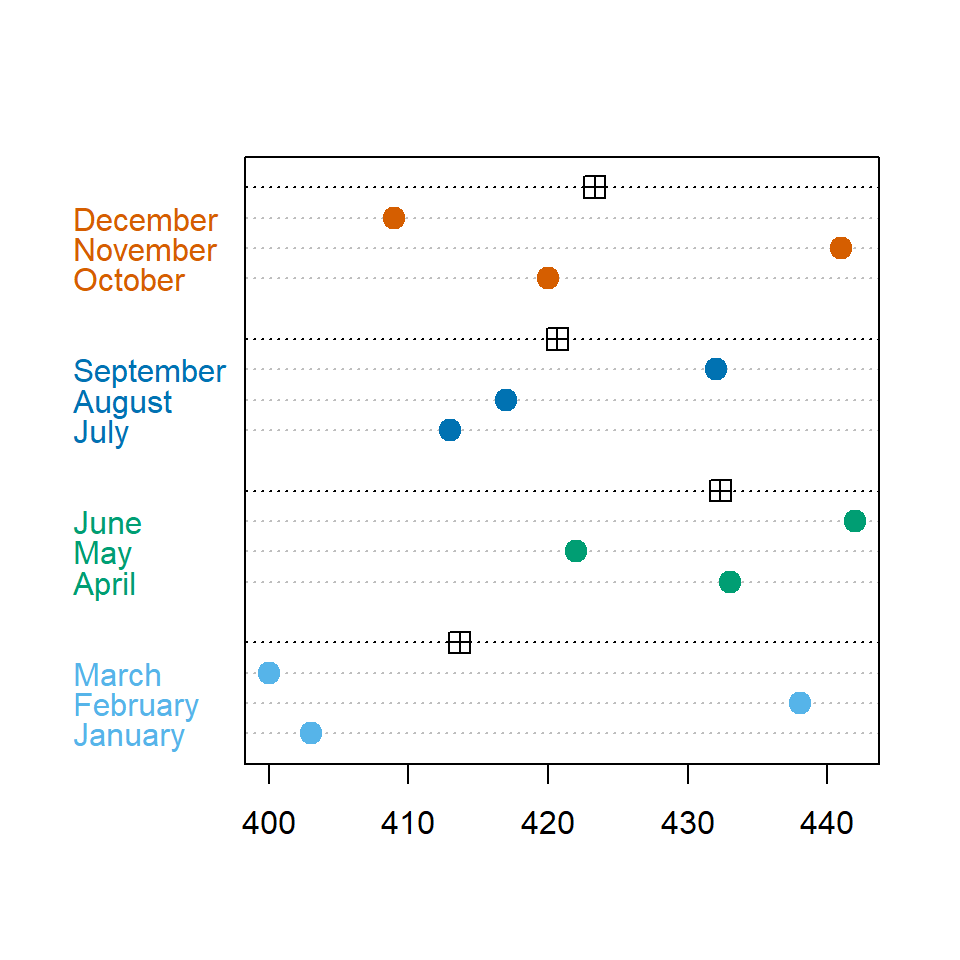

Dot plot by group with colors

The new points added with gdata can be customized with gpch and gcolor arguments, to modify the pch symbol and the color of the new points, respectively.

# Colors for each group
cols <- c(rep("#56B4E9", 3), rep("#009E73", 3),
          rep("#0072B2", 3), rep("#D55E00", 3))

dotchart(sold,
         pch = 19, pt.cex = 1.5,
         labels = month,
         groups = rev(quarter),
         color = cols,
         gdata = rev(tapply(sold, quarter, mean)),
         gpch = 12,
         gcolor = 1)

Order the values

Finally, note that you can order the values and the labels based on the variable or other measure. In the following example we are ordering the months based on the amount of sales.

# Colors for each group
cols <- c(rep("#56B4E9", 3), rep("#009E73", 3),
          rep("#0072B2", 3), rep("#D55E00", 3))

dotchart(sort(sold),
         labels = month[order(sold)],
         pch = 19, pt.cex = 1.5,
         groups = rev(quarter),
         color = cols)

Ordered dot plot in R